
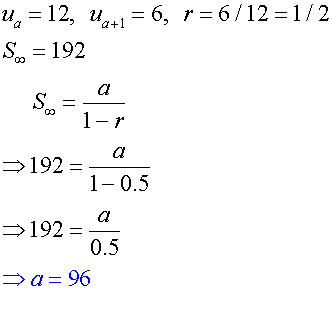
If the rule is to multiply or divide by a specific number each time, it is called a. Throughout this video, we will see how a recursive formula calculates each term based on the previous term’s value, so it takes a bit more effort to generate the sequence. Number sequences are sets of numbers that follow a pattern or a rule. We want to remind ourselves of some important sequences and summations from Precalculus, such as Arithmetic and Geometric sequences and series, that will help us discover these patterns. Let us learn the arithmetic sequence explicit formula, and its.
#Explicit formula for geometric sequence series
Here the arithmetic sequence explicit formula (a n 3n - 1) is useful to find any terms of the series and can be calculated without knowing the previous term. And it’s in these patterns that we can discover the properties of recursively defined and explicitly defined sequences. The formulas applied by this geometric sequence calculator are detailed below while the following conventions are assumed: - the first number of the geometric progression is a - the step/common ratio is r - the nth term to be found in the sequence is a n - The sum of the geometric progression is S. The arithmetic sequence explicit formula for this series is a n a + (n - 1)d, or a n 2 + (n - 1)3 or a n 3n - 1. What we will notice is that patterns start to pop-up as we write out terms of our sequences. All this means is that each term in the sequence can be calculated directly, without knowing the previous term’s value. So now, let’s turn our attention to defining sequence explicitly or generally. Isn’t it amazing to think that math can be observed all around us?īut, sometimes using a recursive formula can be a bit tedious, as we continually must rely on the preceding terms in order to generate the next. In fact, the flowering of a sunflower, the shape of galaxies and hurricanes, the arrangements of leaves on plant stems, and even molecular DNA all follow the Fibonacci sequence which when each number in the sequence is drawn as a rectangular width creates a spiral. For example, 13 is the sum of 5 and 8 which are the two preceding terms. In this case, for example, -50/-25 2, and the ratio is 2. You can guess the ratio by dividing any term by the previous one. Notice that each number in the sequence is the sum of the two numbers that precede it. The general formula for a geometric sequence is: where is the first term, and is the ratio.

And the most classic recursive formula is the Fibonacci sequence. Staircase Analogy Recursive Formulas For SequencesĪlright, so as we’ve just noted, a recursive sequence is a sequence in which terms are defined using one or more previous terms along with an initial condition.


 0 kommentar(er)
0 kommentar(er)
